李惠 / 南京农业大学人文与社会发展学院
摘 要:社会网络分析是整合了社会网络理论、方法和应用的一种范式,已在自然科学、社会科学和人文学科领域得到广泛运用。社会网络分析可以帮助研究者观察网络内部个体或群体的重要关系与行为模式,探索网络全局的组织架构和演变规律。文章从网络研究中常见的无标度现象、中心性度量和社区发现这三个问题入手,研讨具体实施中的注意事项,探究可行的解决路径,以期对相关研究有所助益。
关键词:社会网络分析 数字人文 无标度网络 网络中心性 社区发现
引 言
复杂网络(Complex Networks)是现实世界中复杂系统的拓扑抽象,从数学的角度,可以定义为以多种类型的实体为节点、以实体之间的相互作用关系为边构成的图。比较常见的复杂网络有交通网络、金融网络、社会网络等。社会网络分析(Social Network Analysis,简称SNA)是使用网络和图的相关理论和方法探索社会关系的具体实践,既关注个体行为,也关注网络整体拓扑结构反映的关系模式。
社会网络分析的雏形,现可追溯至19世纪中期社会学的创始人之一、法国哲学家Auguste Comte对社会系统内部关系的研究,“家庭演变成部落,部落演变成国家”。[1]之后,德国教师Johannes Delitsch在1900年用矩阵描述了所任教班级53名男生在1880到1881年间的友谊关系,[2]他发现,学生学业表现的排名与该生的受欢迎程度密切相关。相似的,1934年医学博士Jacob Moreno在所撰的社会计量学著作Who shall Survive[3]中,用社会关系图分析了纽约某感化院中少女之间的关系,以此来制定政策,旨在减少青少年的叛逆行为。社会计量学采用量化研究方法开展实验,旨在探索个人在群体中的地位以及群体的演变规律和组织架构,而这种对社会群体结构的关注正是社会网络研究的核心。到1930年代末,社会网络研究就已具备了社会学家Linton Freeman[4]所定义的现代社会网络分析的四要素:(1)建立结构性的思维直觉;(2)系统性地搜集关系数据;(3)网络结构可视化;(4)构建数学模型和计算模型。随着该领域学者在高校间的工作调动和学术交流、信息技术的发展、国际性会议的召开和学术期刊的创办,社会网络的概念传播至更广泛的学科领域,受到多学科学术权威的认可。
随着数字化数据资源日益丰富,愈来愈多的人文学者开始探索大规模文献的共性特征,以及历史发展中事物之间(如人物、事件、地点、物体、概念等)的相互作用关系,如历史学者Maximilian Schich等[5]在2014年基于两千年间欧洲和北美名人的出生地和死亡地数据,可视化地呈现欧洲从古罗马时期至今的文化名人的迁徙网络;历史学者Ruth Ahnert等[6]基于亨利八世到伊丽莎白一世(1509—1603)九十余年间逾12万封信,构建了都铎王朝英国名人的书信网络;斯坦福大学的Kindred Britain项目,[7]基于1500年间英国约三万人的亲属关系构建的社会网络,以可视化的方式展示了英国名人的家族脉络。由此可见,越来越多的人文学者选择社会网络分析的计算方法,高效地抽取大规模数字化资源中隐含的各种关系,如人物亲属关系、人际交往关系、共现关系等。在此基础上,进而观察事件的演变趋势,为相关学科提供了新的解读视角与研究路径。
现阶段人文领域社会网络分析的研究热点,多为文献中实体关系的抽取和网络可视化的呈现,这两种研究相辅相成,但对计算方法的选取依据和评价标准,尚未有明晰的认知;且许多未参与过“数字人文”研究的人文学者,对网络分析的性质和效果持保留和观望的态度。因此本文从研究中常用的社会网络分析的原理和方法入手,就无标度网络、中心性度量和社区发现这三个方面分析在具体实施中的难点和需注意的要点加以探讨,希望能够促成对社会网络分析更全面、深入的理解,使人文学者在具体应用中有的放矢,将更多的精力投入到问题的提出和结果的阐释当中。
一、无标度网络和幂律分布
关于无标度特性和幂律分布的研究,目前已追溯至意大利经济学家Pareto[8]在19世纪末的财富分布调查,他观察到意大利20%的人口拥有80%的土地资源。受此启发,质量管理学家Juran[9]在20世纪中期提出帕累托法则(Pareto Principle,亦被称为二八定律),即20%的变因导致了约80%的结果,换言之,所有变量中,最重要的仅占少数(20%)。这种“关键少数”现象出现在很多领域:社会关系计量学的创始人Moreno和Jennings[10]在1938年通过理论计算佐证并拓展了社会学家Lazarsfeld的构想,即学生选择伙伴时,会有一个学生被多数人选择,但他/她并不会相应地选择其他人;社会学家Merton[11]提出马太效应(The Matthew Effect),即相比于无名小卒,著名科学家的成果更容易获得认可和嘉奖;经济学家Simon[12]发现不仅在经济领域,在社会和生物领域中也广泛存在指数大于1的幂律分布,即长尾分布;科学计量之父Price[13]指出科学文献的有向引用网络中,节点度遵循幂律分布,且存在累积优势(Cumulative Advantage,也称为优先链接),如引用率较高的文章更易获得新的引用。物理学家Barabási[14]在1999年将互联网所呈现出的类似现象量化为无标度特性,自此相关研究成为热点。
给定网络中,若只有少部分节点具有高度值,而其余节点的度值都很低,这种现象就称为网络的无标度特性(Scale-free Network)。而幂律分布(Power-law Distribution)的通式可写为y=cx-r,其中r为幂指数,c为大于零的常数。幂律分布的共性是只有少数事件的发生率很高,而绝大多数事件的发生率很低。[15]近二十年内,无标度特性和幂律分布在各学科领域构建的网络中均被发现,以我国的数字人文领域为例,集中在现代汉语的词汇网络、语义场网络、人物网络等。但无标度网络是否等同于服从幂律分布的网络,仍处在探讨之中。Clauset等人[16]在2018年对近一千个社交、生物、交通等网络数据集开展幂律检验,发现只有约4%的网络,显示出明显的无标度结构特性。但Barabasi等人[17]放宽了幂律分布的公式定义,对115个网络数据集开展检验,发现无标度网络的比例要明显要高于Clauset的结论。虽然无标度网络的幂律分布尚未有定论,但不同学者多年研究基本可以达成一个共识:多数大规模网络的度分布具有长尾特征,这与数字人文研究中的诸多发现也是一致的。在实际网络分析中,应“粗看长尾、细辨幂律”,[18]对于度分布的幂律检验应设定统一标准,力求严谨。
二、网络中心性
中心性(centrality)是社会网络分析中常用的评价指标,从不同角度刻画了节点在网络中的重要程度。数字人文领域的研究者经常运用中心性的计算方法,识别网络中的中心人物/人物对。本文将常用的中心度、中介中心性、接近中心性和PageRank的计算方法,简述如下。
•中心度(Degree Centrality)。在无权重无向的社会网络中,给定节点的中心度计算为与该节点相接的边的数目。中心度是对节点重要性最直观的描述,但没有关注节点的周边环境(如邻接节点),不够精确。[19]
•中介中心性(Betweenness Centrality)。中介中心性衡量节点在网络中所起到的媒介或者桥梁作用,是对该节点影响力的评价指标。中介中心性越高,该节点对其他节点之间信息传递的控制力越强。给定节点的中介中心性,一般计算为该节点出现在其他节点间的最短路径上的概率。[20]
•接近中心性(Closeness Centrality)。接近中心性关注给定节点与其他节点间的距离。到达其他节点间的距离越短,该节点的接近中心性越高。给定节点的接近中心性,一般计算为该节点到其他所有节点最短路径平均值的倒数。[21]
•PageRank。一个节点的重要程度不仅与自身有关,而且与其邻居节点的重要程度相关。邻居节点在网络中的连接越多,这个节点就越重要。特征向量中心性,一般计算为对应图的邻接矩阵的最大特征向量值。基于特征向量中心性的原理,谷歌创始人Page和Brin在1996年提出PageRank,[22]用于谷歌搜索引擎排序网页搜索结果的算法。该算法认为万维网中一个页面的重要性取决于指向它的其他页面的数量和质量。换言之,如果一个网页被很多重要的网页指向,则这个网页自身也很重要。给定任意节点ti,预设网络中有n个节点(t1,t2,……,tn)都有边指向i,那么采用迭代算法,PageRank可用如下公式计算:
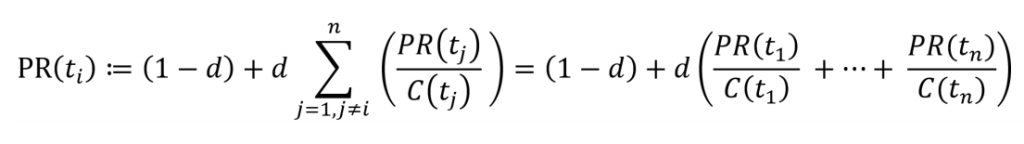
d代表阻尼系数,取值在0和1之间,C(tj)代表节点tj的出度。这些经典的网络中心性计算方法,分别从不同的角度衡量了特定网络中节点的重要性。但在实际的案例分析中,仍存在着争议。
1.不同的中心性计算方法得出的中心节点可能是不一致的,例如经典的风筝网络(Krackhardt Kite Graph)(如图1所示),中心度数值最高的是节点A,中介中心性最高的是节点D,接近中心性最高的是节点B和C。中心度相同的节点,未必在网络中拥有同样重要的地位;其次,在实际网络中,信息有时候并非沿着最短路径流动,而是按意愿随机流动,因而在这些网络中,中介中心性并不适用;再者,接近中心性与中心度高度相关,仅适合于星型网络,并不适合正则图或者随机网络。迄今为止,尚未有统一的标准对各种计算方法开展测评,如何客观准确地评估算法优劣仍为一大挑战。目前较常用的方法有利用节点排序的相关性、网络的鲁棒性(robustness)、传播动力学模型等评价排序算法。但在考虑各种中心性算法结果不一致的前提下,是否可以利用多种方法进行综合评价,得出最优解。比如选取多种计算方法度量网络节点的重要性,对获得的数值标准化,赋予不同的权重,形成最终的排序;又或者使用真实的大规模复杂网络来验证算法得出的重要节点的真实影响力。
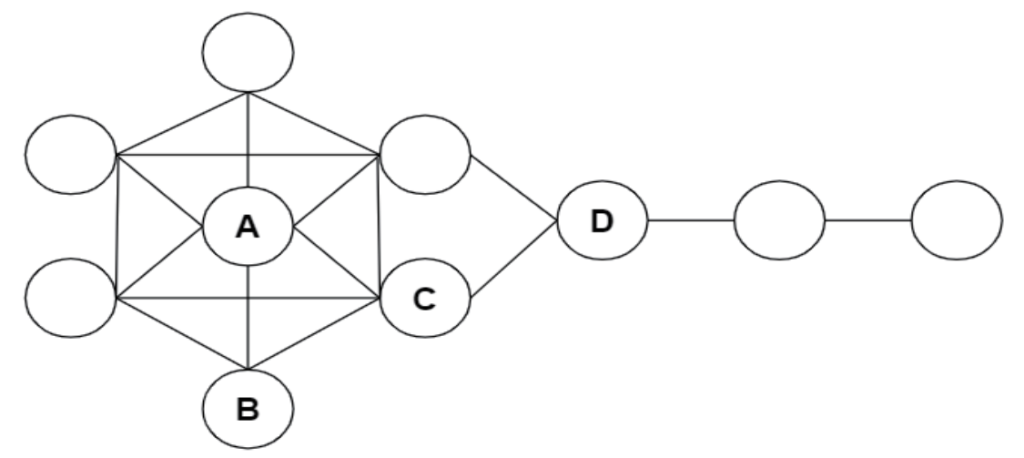
图1 风筝网络(Krackhardt Kite Graph)示例
2.中心性往往聚焦于对网络中(最)重要节点的度量,但对其他节点的评估结果并不一定可靠,如网页搜索常用的PageRank算法,往往只能保证前几个页面排序的准确。[23]关于如何衡量网络中不同等级节点的重要性,Kitsak等人提出用k-shell分解法(k-shell decomposition),根据节点的中心度数值,将节点分离成多层。分解过程简述如下[24]:预设网络中无连接的孤立节点已过滤掉;先将度值为1的节点及其所邻接的边去除,之后再将网络中新出现的度值为1的节点删除,重复上述操作,直至网络中不再有度值为1的节点。所有已被删除的节点和它们所邻接的边组成第一层,称为1-shell (ks=1)。重复上述方法,继续去除网络中剩余中心度为2的节点及其邻边,得到第二层2-shell(ks=2);以此类推,直到网络中的每一个节点都归属于唯一的一层。此方法直观便捷,计算复杂度低,在分析大规模网络的层级结构等方面有很多应用,但有一定局限性,后期陆续有学者对其进行改进,扩大其适用范围并细化排序结果。
3.真实网络常常随着时间和空间不断变化,而节点的重要性也随之变化。目前常用于数字人文研究的经典中心性算法,主要是针对静态网络,并对地域划分不敏感,这会遗失重要的时空信息。现较常用的方法是将时间和空间分开计算,针对时间因素,常将时间网络划分若干时间区间内的子图,将每一个子图看作是一个“拟静态网络”,并开展计算;针对空间网络,同理常根据地图将网络划分成若干区域的子图,对每一个子图分别使用经典算法计算。现也有一些学者兼顾了时间网络中的即时互动行为和空间网络中的地域移动距离,提出了一些融合时空因素的计算方法,但尚未在业界达成共识。
三、社区发现
社区的概念,最早可以追溯至1887年德国社会学家Tönnes提出的“Gemeinschaft”[25]概念,指代一种社会组织形式(“共同体”)。20世纪中期,美国社会学家将其正式对应为英文中的“Community”,[26]中国社会学家将其汉译为社区(后又被译为社群、社团等)。[27]自此,“社区”一词逐渐拓展到诸多领域,如心理学、管理学、网络科学等。与此同时,不同学科的研究者对社区的定义也随之增多。
迄今为止“社区”这一概念并未有明确精准的界定,在网络科学领域,学者们基本可达成的共识为:一个社区的内部节点之间连接的边数,应远高于该社区内部节点与社区外节点的连接边数,[28]换言之,社区内部节点连接的紧密程度应远高于外部。网络中如果包含一定数量的符合上述特征的社区,则称该网络拥有社区结构。社区发现(Community Detection,也译为社区检测)旨在从给定网络中找出社区结构,准确地理解复杂系统的组织原则、拓扑结构与动力学特性。[29]
根据网络中不同社区节点的重叠程度,可将社区划分为重叠社区(Overlapping Community)和非重叠社区(Disjoint Community)。非重叠社区,即网络中每个节点仅属于一个社区,社区之间没有交集。大部分社区发现的经典算法都是面向非重叠社区提出的,在数字人文领域应用较多的为基于模块度的算法,简述如下。
模块度 模块度(Modularity)是Newman于2004年[29]提出的,2006年改进了计算公式[31]并扩大了适用范围。模块度不仅是大量社区发现的算法基础,现也成为评价社区检测的一种常用量化指标。模块度的主要思想为社区内部边数占总边数的比值应大于随机情况下该比值的期望值。实际社区内部边数与期望值的差越大,说明该网络与随机网络的差异越大,换言之,该网络的社区结构越明显。模块度的数值范围在0到1之间,通常认为值越大,社区发现的算法效果越好,划分越合理。但真实网络中的模块度一般取值在0.3到0.7之间。
虽然社区发现的经典算法大多是围绕非重叠社区展开的,但现实世界的复杂网络中,其实大部分的节点存在同时从属于多个社区的情况,比如社会网络中的一个人可能同时属于多个交际圈(亲友圈、工作圈、学习圈等),换言之,这些网络是由重叠社区构成的。与此同时,网络中也存在着一部分节点,不属于任何的社区。这些孤立的节点该如何考量,是否应该看成单个节点组成的若干社区。这时就可以选取凝聚子群的计算方法,来帮助研究者发现不同社区共有的节点和网络中的孤立节点。
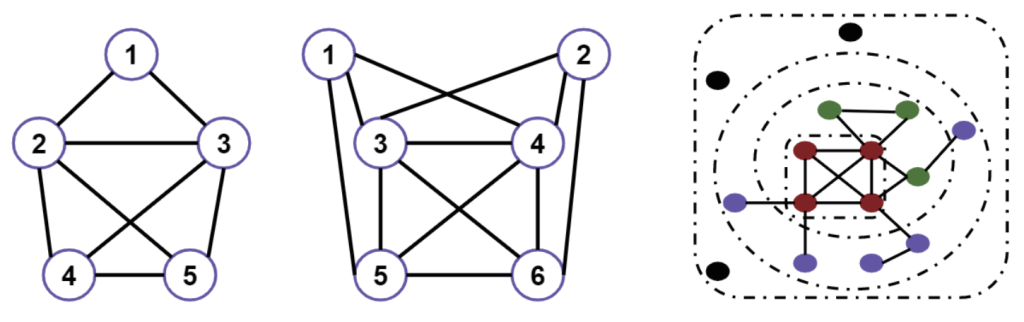
图2 凝聚子群(Cohesive Subgroup)示例
凝聚子群 在社会网络领域,凝聚子群(Cohesive Subgroup)可定义为网络中联系频繁、强烈而直接的节点子集,[32]而分析网络中存在多少这样的子群、子群之间的关系、子群内部节点间的关系等,是凝聚子群分析的主要任务。[33]经典的计算方法有小团体(clique)、K-丛(K-plex)、K-核(K-core)等。小团体[34]指代无向网络中的最大完全子图,子图内部节点之间都有边相连。如图2(a)所示,{2,3,4,5}和{1,2,3}是两个小团体,这两个小团体就存在部分节点(2和3)的重叠。K-丛是指给定包含n个节点的子群内,每个节点至少与其余n-k个节点相连,即每个节点的度数至少为n-k。如图2(b)所示,{3,4,5,6}是一个1丛,{1,3,4,5,6}是一个2丛,{1,2,3,4,5,6}是一个3丛。K-核,[35]是指无向网络中的最大导出子图,该子图内部节点的度不小于数值k。如图2(c)所示,黑色节点层属于该图的0核,为没有连接的孤立节点集合;1核就是去掉孤立节点层的子图,红色节点层为3核。该算法的计算复杂度小,常用于发现网络中的社区结构。
除了上述简介的社区发现算法,目前网络科学领域已涌现出大量的社区发现算法,如Edge Betweenness、Random Walk、Infomap等,那么如何客观地衡量社区发现的优劣度已成为社区发现领域所面临的一个主要问题。[36]目前尚未有统一的标准去评估或比较不同社区发现的算法效果,比较常用的评价指标有标准化互信息、模块度和LRF指标(模块度已在上文中介绍,此处不再赘述)。
1.已知真实社区的划分情况
标准化互信息(Normalized Mutual Information, NMI)[37]常用于聚类任务中,度量两种实验结果的差异程度,后拓展到社区发现领域,评估实验结果与真实划分之间的差异性。NMI是基于混淆矩阵而定义的,具体计算方法简述如下。
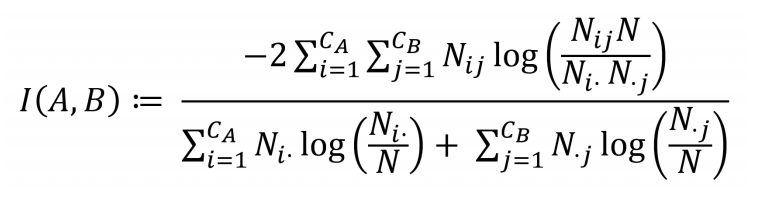
N指代混淆矩阵,该矩阵的行对应真实的社区,数目为CA,列对应于社区发现的算法检测到的社区,数目为CB。Ni.表示矩阵N中第i行的和,N.j表示矩阵N中第j列的和。I(A,B)的数值在0到1之间,若检测到的社区与真实社区一致,I(A,B)=1;若完全不同,I(A,B)=0。数值越大,说明该算法的划分结果越准确。
2.未知真实社区的划分情况
现实生活的复杂网络,由于类型众多,很难掌握其内部的社区划分,考虑到标注数据的规模限制性,若能生成模拟真实网络的人工网络,即可测评社区检测算法的有效性,比较不同算法的优劣程度。Lancichinetti等人基于Girvan和Newman的GN基准,提出LFR基准(Lancichinetti–Fortunato–Radicchi benchmark),[38]在生成随机网络的同时,保证了现实网络中的度分布和社区分布规模的不均衡性。该基准简述如下:
(1)网络中的节点服从指数为γ的幂律分布,度值最小设为kmin,最大设为kmax,保证平均度为<k>。使用配置模型生成给定度分布下的随机网络。
(2)设置混合系数µ,使得每个节点和所在社区占比为1-µ的其余节点相连,并与社区外网络中占比为µ的节点相连。
(3)社区的规模服从指数为β的幂律分布,社区规模最小设为smin,最大设为smax,令smin>kmin且smax>kmax,保证每个节点都能划分入至少一个社区。
(4)起初,所有节点未被分配社区。第一次迭代时,每个节点被随机分配社区;如果一个社区的规模超过该节点的社区内部连接度,该节点加入该社区,否则不加入。此过程不断重复直到所有节点都进入社区。
(5)为了确保社区内部节点的连接满足混合系数µ,需遍历每个节点,对不满足条件的节点进行调整。
在此基础上,再结合标准化互信息NMI对社区发现算法的有效性开展评估。互信息值为1,说明检测到的社区与基准社区完全一致;互信息值为0,说明二者完全不同。
结 论
社会网络分析打破了传统的学科界限,将社会科学(如社会学、心理学、新闻学等)、自然科学(数学、生物、物理等)和人文学科(如艺术学、文学、语言学、历史学等)等诸多领域的学者汇聚到一起,共同探索复杂系统内部的网络特性。这种跨学科的融合,会拓宽视野、创新见解,促进知识的更新与发展。在人文研究中,学者们已经从文本、图像、音频等大规模数据中,抽取关系数据构建复杂网络,网络中的节点代表各种实体,边代表实体间的关系。节点和边均可附加属性,如与节点相关的地点、时间等信息可作为节点属性,节点之间的紧密程度可量化为边属性,而边的方向性则说明了信息的传播指向。这种网络建模的思想,可以帮助学者将散落在多张表、多个库中的数据连接起来并予以整合,以一种全局的思想观察并分析实体关系和社会行为的预设模式与规则。美中不足的是,很多研究以画出漂亮的网络图为目的,止步于“可视化”,[39]对网络的深层探索尚为数不多。本文聚焦于无标度网络特性、中心性度量及社区发现与评估这三方面,针对具体实施中的难点,提出可行的解决方案,为人文学者在社会网络分析的实际应用中提供参考。
Some Thoughts on Social Network Analysis and its Use Cases in Humanities
Li Hui
Abstract: Social Network Analysis is a paradigm that integrates theories, methods and applications of social networks. It is widely applied in the research area of natural science, social science and humanities. Social network analysis can help researchers to scrutinize the relationships and behavioral patterns of individuals or groups within the network, and also to explore the organizational structure and evolutionary patterns of the whole network. This paper discusses the methods and considerations of scale-free networks, centrality measures, and community detection, which are frequently used in network research.
Keywords: Social Network Analysis; Digital Humanities; Scale-free Network; Network Centrality; Community Detection
(编辑:赵薇)
注释:
[1]Harriet Martineau, The Positive Philosophy of Auguste Comte, v. 2, Kitchener: Batoche Books, 2000, p. 234.
[2]Johannes Delitsch, “Über Schülerfreundschaften in einer Volksschule,”Zeitschrift für Kinderforschung,
vol. 5, 1900, pp. 150-162.
[3]Jacob L. Moreno, Who Shall Survive, Washington DC: Nervous and Mental Disease Publishing, 1934.
[4]Linton Freeman, The Development of Social Network Analysis: A Study in the Sociology of Science, New York: Empirical Press, 2004, p. 3.
[5]Maximilian Schich et al., “Network Framework of Cultural History,”Science, vol. 345, no. 6196, 2014, pp.
558-562.
[6]Tudor Networks, http://tudornetworks.net/, accessed June 1, 2021.
[7]Kindred Britain, https://kindred.stanford.edu/notes.html, accessed June 1, 2021.
[8]Vilfredo Pareto, Cours d’Économie Politique, vol. I, Lausanne: F. Rouge, 1896, p. 430; Vilfredo Pareto, Cours d’Économie Politique, vol. II, 1897, p. 426.
[9]Joseph Juran, “Pioneer in Quality Control,” https://www.nytimes.com/2008/03/03/business/03juran. html, accessed June 1, 2021.
[10]J. L. Moreno, H. H. Jennings, “Statistics of Social Configurations,”Sociometry, vol. 1, 1938, pp. 342-374.
[11]R. K. Merton, “The Matthew Effect in Science: The Reward and Communication Systems of Science are Considered,”Science, vol. 159, no. 3810, 1968, pp. 56-63.
[12]H. A. Simon, “On a Class of Skew Distribution Functions,”Biometrika, vol. 42, no. 3/4, 1955, pp. 425-440.
[13]D. J. de S. Price, “Networks of Scientific Papers,”Science, vol. 149, no. 3683, 1965, pp. 510-515.
[14]A. L. Barabási, R. Albert, “Emergence of Scaling in Random Networks,”Science, vol. 286, no. 5439, 1999, pp. 509-512.
[15]胡海波、王林:《幂律分布研究简史》,《物理》2005年第12期。
[16]A. D. Broido, A. Clauset, “Scale-free Networks are Rare,”Nature Communications, vol. 10, no. 1017, 2019, pp. 1-10.
[17]I. Voitalov et al.,“Scale-free Networks Well Done,”Physical Review Research, vol. 1, no. 3, 2019, DOI:10.1103/PhysRevResearch.1.033034.
[18]汪小帆:《无标度网络研究纷争:回顾与评述》,《电子科技大学学报》2020年第4期。
[19]任晓龙、吕琳媛:《网络重要节点排序方法综述》,《科学通报》2014年第13期。
[20]G. A. Barnett, Encyclopedia of Social Networks, Thousand Oaks: SAGE Publications, 2011, p. 34.
[21]H. Liu, M. A. Abbasi, R. Zafarani, Social Media Mining: An Introduction, Cambridge: Cambridge University Press, 2014, p. 61.
[22]L. Page, S. Brin, “The Anatomy of a Large-scale Hypertextual Web Search Engine,”Computer Networks and ISDN Systems, vol. 30, no. 1-7, 1998, pp. 107-117.
[23]G. Ghoshal, A. L. Barabási, “Ranking Stability and Super-stable Nodes in Complex Networks,”Nature Communications, vol. 2, no. 1, 2011, pp. 1-7.
[24]任卓明等:《复杂网络中最小K-核节点的传播能力分析》,《物理学报》2013年第10期。
[25]F. Tönnes, Gemeinschaft und Gesellschaft: Abhandlung des Communismus und des Socialismus als Empirischer Culturformen, Leipzig: Fues, 1887.
[26]C. P. Loomis, Community and Society, London: Routledge, 1988.
[27]黄兆临:《关于社会学名词的翻译》,《晨报·社会研究》1934年4月11日。
[28]S. Fortunato, D. Hric, “Community Detection in Networks: a User Guide,” 2016, pp. 1-44, DOI: 10.1016/j.physrep.2016.09.002.
[29]骆志刚等:《复杂网络社团发现算法研究新进展》,《国防科技大学学报》2011年第1期。
[30]M. E. J. Newman, M. Girvan, “Finding and Evaluating Community Structure in Networks,”Physical Review E, vol. 69, no. 2, 2003, https://arxiv.org/abs/cond-mat/0308217.
[31]M. E. J. Newman, “Modularity and Community Structure in Networks,” Proceedings of the National Academy of Sciences, vol. 103, no. 23, 2006, pp. 8577-8582.
[32]S. Wasserman, K. Faust, Social Network Analysis: Methods and Applications, Cambridge: Cambridge University Press, 1994, p. 250.
[33]朱庆华、李亮:《社会网络分析法及其在情报学中的应用》,《情报理论与实践》2008年第2期。
[34]R. D. Luce, A. D. Perry, “A Method of Matrix Analysis of Group Structure,”Psychometrika, vol. 14, no. 2, 1949, pp. 95-116.
[35]S. B. Seidman, “Network Structure and Minimum Degree,”Social Networks, vol. 5, no. 3, 1983, pp. 269-287.
[36]阳广元等:《国内社区发现研究进展》,《情报资料工作》2014年第2期。
[37]L. Danon et al., “Comparing Community Structure Identification,”Journal of Statistical Mechnics: Theroy and Experiment, vol. 9, 2005, DOI: 10.1088/1742-5468/2005/09/P09008.
[38]A. Lancichinetti, S. Fortunato, and F. Radicchi, “Benchmark Graphs for Testing Community Detection Algorithms,”Physical Review E, vol. 78, no. 4, 2008, DOI: https://doi.org/10.1103/PhysRevE.78.046110.
[39]严程:《现代文学研究的“数字人文”方法刍议》,《现代中文学刊》2019年第1期。

